एक समद्विबाहु त्रिभुज का क्षेत्र कैसे प्राप्त करें

इससे पहले कि आप इस सवाल का जवाब देना शुरू करें कि कैसे ढूंढेंएक समद्विबाहु त्रिभुज का क्षेत्रफल और लेख के व्यावहारिक भाग पर जाना है, जहां सूत्र और गणना दी गई है, आइए हम स्वयं के लिए बहुत ही अवधारणा को दर्शाते हैं। एक समद्विबाहु त्रिकोण एक त्रिकोण है जिसमें तीन पक्षों में से दो लंबाई में समान हैं, जिसे पार्श्व पक्ष कहा जाता है एक नियमित त्रिकोण के मामले में, जहां सभी पक्ष बराबर हैं, यह समद्विबाहु भी माना जाता है, लेकिन इसके विपरीत, जब एक समद्विबाहु त्रिकोण सही माना जाता है - झूठा है

त्रिकोण के पक्षों को नामित किया जाना चाहिए, हम इसे इस तरह से करेंगे, जैसा कि नीचे दिए गए चित्र में दिखाया गया है, जहां: एक - पक्ष, बी-बेस और एच-ऊंचाई

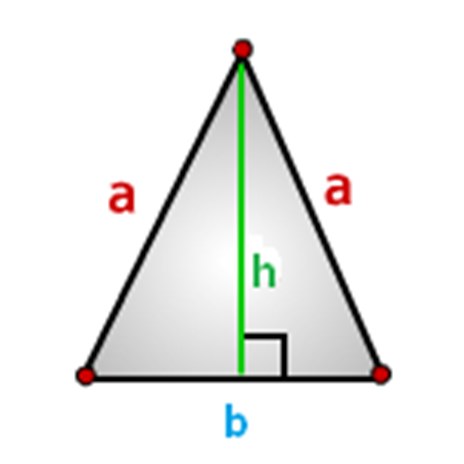
एक समद्विबाहु त्रिकोण के क्षेत्र की गणना कैसे करें, सूत्र

हम ऊंचाई, पक्ष और कोण का नेशनल बनाने के बाद, हम समस्या को हल करना शुरू कर सकते हैं।

शुरू करने के लिए, हम यह निर्धारित करेंगे कि हम क्या जानते हैं।

यदि ऊंचाई और नीचे - तो शास्त्रीय सूत्र (* - गुणा साइन):

एस = ½ * बी * एच

चलो, उदाहरण के लिए, संख्याएं जहां: h = 16, b = 18, हम निम्नलिखित प्राप्त करते हैं:

एस = आधा * 18 * 16 = 9 * 16 = 144;

एक समद्विबाहु त्रिभुज का क्षेत्र S = 144 cm2 है

ऐसे अन्य सूत्र भी हैं जो हमारी मदद करेंगेएक समद्विबाहु त्रिभुज के क्षेत्र को कैसे जानने के लिए ऐसा ही एक सूत्र हेरोन की विधि है। चलो एक जटिल सूत्र नहीं लिखते हैं, हम एक आधार के लिए लेते हैं, एक छोटा:

एस = ¼ बी √4 * ए 2-बी 2

यह स्पष्ट है कि बी आधार है, और - समान पक्ष सूत्र उस मामले में उपयुक्त है जहां एच-ऊंचाई अज्ञात है।

मूल्यों को प्रतिस्थापित करना, एक = 6, बी = 3 दें, हमें निम्न प्राप्त होते हैं:

एस = ¼ * 3 √4 * 62-32 = ¾ √144-9 = ¾ * 9 = 8,7

आप त्रिभुज के किनारों के बराबर क्षेत्र और पक्षों के बीच के कोण की गणना करने के लिए उपयोग कर सकते हैं:

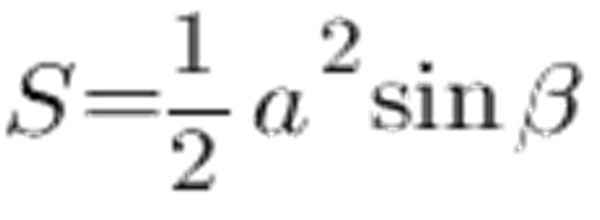
साइन टेबल के अनुसार, कोण 45 डिग्री के बराबर 0.7071 बराबर है, और इसे 6 सेमी होने दें, हम निम्न प्राप्त करते हैं:

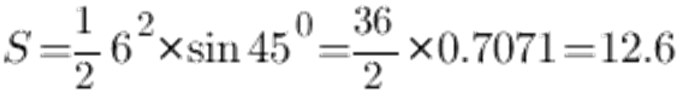
नतीजतन, एक समद्विबाहु त्रिकोण का क्षेत्रफल 12.6 सेमी 2 है।

यहां क्षेत्र सहित, गणना करने के तरीके भी शामिल हैंएक समद्विबाहु त्रिकोण के मामले में, लेकिन वे जटिल नहीं हैं और जटिल गणित की धारणा में "प्राथमिक" गणनाओं, जैसे कि ऊपर दी गई, पर लागू नहीं होते हैं। और उन चीजों के बारे में बात करना उचित नहीं है, जो अनुभव के साथ शिक्षक भी नहीं समझेंगे।

तो, आप इस पर राहत की सांस ले सकते हैंएक समद्विबाहु त्रिभुज के क्षेत्र को खोजने के लिए ज्यामिति का एक छोटा सा कोर्स पूरा होगा, और लेख पढ़ने के परिणामस्वरूप प्राप्त ज्ञान "पांच" द्वारा सीखा जाएगा